Mozgások
2006.02.2.
Egy jármű sebesség-idő grafikonját mutatja az alábbi ábra.
a) Jellemezze röviden a jármű mozgását!
b) Mekkora utat tesz meg a jármű 130 másodperc alatt?
c) Határozzuk meg a jármű gyorsulását az egyes útszakaszokon!
a) Jellemezze röviden a jármű mozgását!
b) Mekkora utat tesz meg a jármű 130 másodperc alatt?
c) Határozzuk meg a jármű gyorsulását az egyes útszakaszokon!
2006.10.1.
Egy sportkocsi a reklám szerint 10,6 s alatt gyorsul fel álló helyzetből 100 km/h
sebességre.
a) Mekkora úton gyorsul fel a kocsi erre a sebességre?
b) Mekkora az autó lassulása hirtelen fékezéskor, ha a fékút 72 km/h sebességről álló helyzetig lefékezve 50 méter?
(Feltételezzük, hogy a jármű mindkét vizsgált esetben egyenes vonalú, egyenletesen változó mozgást végez.)
a) Mekkora úton gyorsul fel a kocsi erre a sebességre?
b) Mekkora az autó lassulása hirtelen fékezéskor, ha a fékút 72 km/h sebességről álló helyzetig lefékezve 50 méter?
(Feltételezzük, hogy a jármű mindkét vizsgált esetben egyenes vonalú, egyenletesen változó mozgást végez.)
2012.06.1.
A képen a reakcióidő megmérésére alkalmas kísérletet látunk.
A mérés során egy vonalzót lógatunk le a végénél fogva.
Társunk a vonalzó alsó végénél, a 0 cm jelzésnél tartja két ujját nyitva, a vonalzó elkapására készen.
Majd hirtelen elengedjük a vonalzót, a társunk pedig,amikor ezt észleli, megpróbálja ujjai összezárásával elkapni azt.
Kezét eközben függőlegesen nem mozgathatja!
A vonalzóról leolvasható, hogy hány cm-nél sikerült elkapnia.
Ily módon megállapítható, hogy mennyi idő telt el a vonalzó leejtése és ujjainak összezárása között, azaz lényegében társunk reakcióideje vált mérhetővé. Hárman tesznek próbát segítségünkkel.
a) Az első játékos reakcióideje 0,15 s. Hol fogja elkapni a vonalzót?
b) A második játékos a 20 cm-es jelnél kapta el a vonalzót.
Mekkora a reakcióideje?
Milyen gyorsan halad a vonalzó az elkapás pillanatában?
c) A harmadik játékos reakcióideje az első játékosénak duplája. Elkapja-e a vonalzót, és ha igen, hol?
g = 10 m/s2, a vonalzó hossza L = 30 cm.
Társunk a vonalzó alsó végénél, a 0 cm jelzésnél tartja két ujját nyitva, a vonalzó elkapására készen.
Majd hirtelen elengedjük a vonalzót, a társunk pedig,amikor ezt észleli, megpróbálja ujjai összezárásával elkapni azt.
Kezét eközben függőlegesen nem mozgathatja!
A vonalzóról leolvasható, hogy hány cm-nél sikerült elkapnia.
Ily módon megállapítható, hogy mennyi idő telt el a vonalzó leejtése és ujjainak összezárása között, azaz lényegében társunk reakcióideje vált mérhetővé. Hárman tesznek próbát segítségünkkel.
a) Az első játékos reakcióideje 0,15 s. Hol fogja elkapni a vonalzót?
b) A második játékos a 20 cm-es jelnél kapta el a vonalzót.
Mekkora a reakcióideje?
Milyen gyorsan halad a vonalzó az elkapás pillanatában?
c) A harmadik játékos reakcióideje az első játékosénak duplája. Elkapja-e a vonalzót, és ha igen, hol?
g = 10 m/s2, a vonalzó hossza L = 30 cm.
2003.1.
A 108 km/h sebességgel egyenes úton haladó gépkocsi vezetőjének reakcióideje 0,1 s.
A vezető akkor észleli az akadályt az úton, amikor az 95 m-re van tőle.
A gépkocsi legnagyobb lassulása –5 m/s2.
Az akadálytól mekkora távolságra tud megállni?
Mi történik, ha a vezető fáradt, és reakcióideje 0,2 s?
A vezető akkor észleli az akadályt az úton, amikor az 95 m-re van tőle.
A gépkocsi legnagyobb lassulása –5 m/s2.
Az akadálytól mekkora távolságra tud megállni?
Mi történik, ha a vezető fáradt, és reakcióideje 0,2 s?
2006.05.1.
Egy 50 g tömegű nyílvesszőt 20 m/s sebességgel függőlegesen felfelé lövünk ki.
a) Milyen magasra emelkedik a nyílvessző?
b) Milyen magasan lesz, és mekkora mozgási energiával rendelkezik a nyílvessző 1 másodperccel kilövése után?
(A közegellenállástól tekintsünk el; g = 10 m/s2.)
a) Milyen magasra emelkedik a nyílvessző?
b) Milyen magasan lesz, és mekkora mozgási energiával rendelkezik a nyílvessző 1 másodperccel kilövése után?
(A közegellenállástól tekintsünk el; g = 10 m/s2.)
2009.06.1.
Egy m = 5 kg tömegű test L =1m hosszúságú
zsinóron, függőleges síkban forog. A forgás sebessége
olyan, hogy amikor a test a körpálya legfelső pontján
tartózkodik, a kötélben éppen nem ébred erő.
g =10 m/s2
a) Mekkora a test pályamenti sebessége a körpálya legfelső pontján?
b) Mekkora a test pályamenti sebessége a körpálya legalsó pontján?
c) Mekkora a kötélben ébredő erő a körpálya legalsó pontján?
g =10 m/s2
a) Mekkora a test pályamenti sebessége a körpálya legfelső pontján?
b) Mekkora a test pályamenti sebessége a körpálya legalsó pontján?
c) Mekkora a kötélben ébredő erő a körpálya legalsó pontján?
2007.06.2.
Egy 0,8 m hosszúságú fonálinga szabad végén 0,2 kg tömegű, elhanyagolható méretű golyó van.
Az ingát vízszintes helyzetbe kitérítik, majd lökés nélkül elengedik.
a) Mekkora sebességgel halad a golyó az inga függőleges helyzetében?
b) Határozzuk meg a golyó centripetális gyorsulását az inga függőleges helyzetében!
(Legyen g = 10 m/s2! A közegellenállás hatását elhanyagolhatjuk. Az inga függőleges helyzetében, a vizsgált pillanatban, a mozgás egyenletes körmozgásnak tekinthető.)
Az ingát vízszintes helyzetbe kitérítik, majd lökés nélkül elengedik.
a) Mekkora sebességgel halad a golyó az inga függőleges helyzetében?
b) Határozzuk meg a golyó centripetális gyorsulását az inga függőleges helyzetében!
(Legyen g = 10 m/s2! A közegellenállás hatását elhanyagolhatjuk. Az inga függőleges helyzetében, a vizsgált pillanatban, a mozgás egyenletes körmozgásnak tekinthető.)
2016.06.2.
Egy mai modern autó mind a négy kerekét egy-egy tárcsafék fékezi.
A tárcsafékek a tárcsa és a fékbetét közti súrlódás segítségével az autó mozgási energiáját hővé alakítják át.
Egy utasokkal együtt 1,2 tonna tömegű autóban egy-egy tárcsafék tömege 9 kg (ez a féktárcsa és a rajta súrlódó fékbetét együttes tömege).
Az autópályán egy fékezés során az autó teljes megállásáig a fékek 60 °C-kal melegedtek fel.
Túllépte-e az autó a 130 km/h sebességkorlátozást, ha a fékek anyagának fajhője c = 400 J/kg C ?
(Tegyük fel, hogy a fékerő mind a négy keréken egyforma volt.
Mivel a fékezés rövid ideig tartott, a fékezéskor a környezetnek leadott hőmennyiségtől eltekinthetünk.)
Egy utasokkal együtt 1,2 tonna tömegű autóban egy-egy tárcsafék tömege 9 kg (ez a féktárcsa és a rajta súrlódó fékbetét együttes tömege).
Az autópályán egy fékezés során az autó teljes megállásáig a fékek 60 °C-kal melegedtek fel.
Túllépte-e az autó a 130 km/h sebességkorlátozást, ha a fékek anyagának fajhője c = 400 J/kg C ?
(Tegyük fel, hogy a fékerő mind a négy keréken egyforma volt.
Mivel a fékezés rövid ideig tartott, a fékezéskor a környezetnek leadott hőmennyiségtől eltekinthetünk.)
2015.06.1.
A NASA 132 méter mély, légüres ejtőcsövében felülről kezdősebesség nélkül elejtenek egy kapszulát.
Ezzel egyidőben alulról is fellőnek egyet.
A két kapszula pontosan félúton találkozik.
a) Mekkora az elejtett kapszula sebessége a találkozáskor?
b) Mekkora kezdősebességgel kellett az alulról indított kapszulát fellőni ahhoz, hogy pontosan félúton találkozzanak?
c) Mekkora volt az alulról indított kapszula sebessége a találkozáskor?
g = 9,8 m/s2
Ezzel egyidőben alulról is fellőnek egyet.
A két kapszula pontosan félúton találkozik.
a) Mekkora az elejtett kapszula sebessége a találkozáskor?
b) Mekkora kezdősebességgel kellett az alulról indított kapszulát fellőni ahhoz, hogy pontosan félúton találkozzanak?
c) Mekkora volt az alulról indított kapszula sebessége a találkozáskor?
g = 9,8 m/s2
2018.06.1.
Egy sík felületen mozgó, pontszerű test egy adott pontból a t = 0 időpillanatban indul el.
Sebességének nagysága v = 10 m/s, gyorsulásának nagysága a = 6 m/s2 .
A mozgás során mindkét mennyiség nagysága végig állandó marad.
a) Milyen mozgást végez a test?
b) Mikor ér vissza a test a kiindulási pontba, és mozgása során mekkora lesz a legnagyobb távolsága ettől a ponttól?
Sebességének nagysága v = 10 m/s, gyorsulásának nagysága a = 6 m/s2 .
A mozgás során mindkét mennyiség nagysága végig állandó marad.
a) Milyen mozgást végez a test?
b) Mikor ér vissza a test a kiindulási pontba, és mozgása során mekkora lesz a legnagyobb távolsága ettől a ponttól?
Lendület
2007.05.2.
Két 10 kg tömegű kiskocsi áll egymással szemben egy egyenes, vízszintes úton, s mindegyikben egy 60 kg tömegű ember ül.
Az egyik kiskocsiban egy 5 kg-os medicinlabda is található, melyet a kocsiban lévő ember átdob a másik embernek.
A labda vízszintes irányú sebessége 8,4 m/s a földhöz képest.
a) Mekkora sebességgel mozog a földhöz képest az egyik kiskocsi az után, hogy utasa eldobta a labdát, s mekkorával a másik, miután utasa elkapta azt?
Mekkora lesz a sebességük egymáshoz képest az után, hogy a labda átkerült a másik kocsiba?
b) Legalább mekkora munkát végzett a medicinlabdát elhajító ember?
Az egyik kiskocsiban egy 5 kg-os medicinlabda is található, melyet a kocsiban lévő ember átdob a másik embernek.
A labda vízszintes irányú sebessége 8,4 m/s a földhöz képest.
a) Mekkora sebességgel mozog a földhöz képest az egyik kiskocsi az után, hogy utasa eldobta a labdát, s mekkorával a másik, miután utasa elkapta azt?
Mekkora lesz a sebességük egymáshoz képest az után, hogy a labda átkerült a másik kocsiba?
b) Legalább mekkora munkát végzett a medicinlabdát elhajító ember?
2014.06.1.
Egy 60 kg tömegű atléta 7,2 km/h sebességgel mozog, amikor felé löknek egy 10 kg tömegű, 10,8 km/h sebességű bevásárlókocsit.
Az atléta a kocsi közeledtével felugrik, s a kocsiban landol. (A felugrás közben megtartja korábbi vízszintes sebességét.)
a) Milyen irányban és mekkora sebességgel fog haladni ezután a kocsi a benne lévő atlétával együtt?
b) Mennyit változott az atléta, illetve a kocsi mozgási energiája?
Az atléta a kocsi közeledtével felugrik, s a kocsiban landol. (A felugrás közben megtartja korábbi vízszintes sebességét.)
a) Milyen irányban és mekkora sebességgel fog haladni ezután a kocsi a benne lévő atlétával együtt?
b) Mennyit változott az atléta, illetve a kocsi mozgási energiája?
2004.1.
Egy modellvasút 30 dkg tömegű mozdonya 2 m sugarú körpályán egyenletesen halad.
Egy teljes kört 3,7 s alatt tesz meg.
a) Mekkora a mozdony sebessége és lendülete?
b) Mekkora oldalirányú erővel nyomja a sín a mozdony kerekét?
c) Legfeljebb milyen magas lejtőre tud felgurulni a mozdony a feladatban szereplő kezdeti lendülettel, ha motorját a lejtő alján kikapcsolják?
(g = 10m/s2 közelítő érték használható.)
Egy teljes kört 3,7 s alatt tesz meg.
a) Mekkora a mozdony sebessége és lendülete?
b) Mekkora oldalirányú erővel nyomja a sín a mozdony kerekét?
c) Legfeljebb milyen magas lejtőre tud felgurulni a mozdony a feladatban szereplő kezdeti lendülettel, ha motorját a lejtő alján kikapcsolják?
(g = 10m/s2 közelítő érték használható.)
Erők
2005.05.1.
Egyik végénél felfüggesztett rugóra 2 kg tömegű testet erősítünk.
Ekkor a rugó megnyúlása 10 cm. (g = 10 m/s2 )
a) Mekkora a rugó rugóállandója?
b) Mennyi munkát végzünk, amíg további 5 cm-rel megnyújtjuk a rugót?
Ekkor a rugó megnyúlása 10 cm. (g = 10 m/s2 )
a) Mekkora a rugó rugóállandója?
b) Mennyi munkát végzünk, amíg további 5 cm-rel megnyújtjuk a rugót?
2016.06.1.
Egy liftben állunk, és éppen akkor próbáljuk meg odébb húzni a bőröndünket, amikor a lift 1,5 m/s2 gyorsulással elindul fölfelé.
Mekkora vízszintes irányú erőt kell a bőröndre kifejtenünk, hogy meg tudjuk mozdítani, ha a tömege 24 kg, a lift padlója és a bőrönd között a tapadási súrlódási együttható 0,5?
g = 9,8 m/s2
Mekkora vízszintes irányú erőt kell a bőröndre kifejtenünk, hogy meg tudjuk mozdítani, ha a tömege 24 kg, a lift padlója és a bőrönd között a tapadási súrlódási együttható 0,5?
g = 9,8 m/s2
2022.10.B.1.
Egyes vidámparkokban megtalálható játék az óriáscentrifuga, melyben gyors forgás közben az emberek a függőleges falra tapadnak, és nem esnek le, miközben a lábuk
alól lesüllyesztik a talajt.
a) Rajzolja le oldalnézetből, ahogy egy ember a centrifuga függőleges falára „tapad”, miközben az forog! Rajzolja be az emberre ható erőket és ezek eredőjét!
Milyen erő akadályozza meg, hogy az ember a fal mentén lecsússzon?
b) Mekkora a minimális tapadási együttható a centrifuga fala és az emberek között, ha a centrifuga, amivel a jelenség megvalósítható, 5 m átmérőjű és 0,5 Hz fordulatszámmal működik?
(g = 9,8 m/s2 )
a) Rajzolja le oldalnézetből, ahogy egy ember a centrifuga függőleges falára „tapad”, miközben az forog! Rajzolja be az emberre ható erőket és ezek eredőjét!
Milyen erő akadályozza meg, hogy az ember a fal mentén lecsússzon?
b) Mekkora a minimális tapadási együttható a centrifuga fala és az emberek között, ha a centrifuga, amivel a jelenség megvalósítható, 5 m átmérőjű és 0,5 Hz fordulatszámmal működik?
(g = 9,8 m/s2 )
Egyensúly
2010.10.1.
Egy 50 méter magas antennát három ponton rögzítenek erős drótsodronnyal.
A rögzítési pontok R = 20 méter sugarú kör mentén helyezkednek el, egymástól egyenlő távolságra.
a) Összesen mekkora erővel húzza lefelé a három rögzítősodrony az antennát, ha mindegyikben 5000 N erő ébred?
b) Miért célszerű a sodronyokat egy kör mentén, egymástól egyenlő távolságra rögzíteni a földhöz?
A rögzítési pontok R = 20 méter sugarú kör mentén helyezkednek el, egymástól egyenlő távolságra.
a) Összesen mekkora erővel húzza lefelé a három rögzítősodrony az antennát, ha mindegyikben 5000 N erő ébred?
b) Miért célszerű a sodronyokat egy kör mentén, egymástól egyenlő távolságra rögzíteni a földhöz?
2011.06.1.
Egy szabályos hasáb alakú, homogén gerenda egyik vége a fal mellett a földön nyugszik, másik végét egy függőleges kötél tartja.
A gerenda a földdel α = 30o-os szöget zár be, tömege 20 kg, hossza 3 m. (g = 10 m/s2 )
a) Mekkora a kötélerő? ( a) ábra )
b) A kötél helyett a gerendát egy ember tartja az eredeti helyzetben, úgy, hogy kezének nyomóereje merőleges a gerendára. ( b) ábra )
Mekkora ez a nyomóerő?
A gerenda a földdel α = 30o-os szöget zár be, tömege 20 kg, hossza 3 m. (g = 10 m/s2 )
a) Mekkora a kötélerő? ( a) ábra )
b) A kötél helyett a gerendát egy ember tartja az eredeti helyzetben, úgy, hogy kezének nyomóereje merőleges a gerendára. ( b) ábra )
Mekkora ez a nyomóerő?
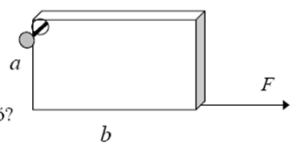
2007.10.1.
Egy téglalap alakú, homogén lemezt az egyik csúcsánál egy szöggel felfüggesztünk, amely körül könnyen elfordulhat a lemez, a vele átellenes csúcsánál pedig vízszintes
irányban F = 6 N erővel húzzuk.
Ekkor a lemez b oldala vízszintes lesz.
a = 30 cm, b = 90 cm ( g = 10m/s2 )
a) Mekkora a lemez tömege?
b) Mekkora a lemezre ható nehézségi erő és a húzóerő eredője?
c) Mekkora a felfüggesztési pontban ható kényszererő?
Ekkor a lemez b oldala vízszintes lesz.
a = 30 cm, b = 90 cm ( g = 10m/s2 )
a) Mekkora a lemez tömege?
b) Mekkora a lemezre ható nehézségi erő és a húzóerő eredője?
c) Mekkora a felfüggesztési pontban ható kényszererő?
2009.05.1.
Az ábrán látható elrendezésben két testet helyezünk egy kétkarú mérleg két karjára, és az egyikhez csigán átvetett fonalat erősítünk.
A mérleg karja súlytalannak tekinthető!
Adatok: m1 = 10 kg , m2 = 2 kg , k1 = 1 m, k2 = 2,5 m, g =10 m/s2
a) Mekkora F erővel kell húznunk a fonalat, hogy a rendszer egyensúlyban legyen?
b) Hová kell tennünk az 2 m testet, hogy F = 75 N erő legyen szükséges az egyensúly fenntartásához?
A mérleg karja súlytalannak tekinthető!
Adatok: m1 = 10 kg , m2 = 2 kg , k1 = 1 m, k2 = 2,5 m, g =10 m/s2
a) Mekkora F erővel kell húznunk a fonalat, hogy a rendszer egyensúlyban legyen?
b) Hová kell tennünk az 2 m testet, hogy F = 75 N erő legyen szükséges az egyensúly fenntartásához?
2011.05.1.
Egy 60 kg tömegű gerenda (homogén hasáb) egy éken nyugszik.
Az alátámasztásaz egyik végtől 1m-re, a másiktól 1,5 m-re van.
A levegőben lévő végre m tömegű testet téve a gerenda átbillen.
(A gerenda vastagsága elhanyagolható a hosszához képest.)
Mekkora ez a tömeg? (g = 10m/s2 )
Az alátámasztásaz egyik végtől 1m-re, a másiktól 1,5 m-re van.
A levegőben lévő végre m tömegű testet téve a gerenda átbillen.
(A gerenda vastagsága elhanyagolható a hosszához képest.)
Mekkora ez a tömeg? (g = 10m/s2 )
2010.06.2.
Egy függőleges tengely körül forgó, vízszintes síkú korongon a tengelytől R = 1 m távolságra m = 2 kg tömegű test helyezkedik el.
A test a koronghoz képes nyugalomban van, azzal együtt forog f = 0,4 Hz frekvenciával.
a) Mekkora a test és a korong közt ébredő tapadási erő?
b) Legalább mekkora a korong és a test között a tapadási együttható?
(g = 10 m/s2 )
A test a koronghoz képes nyugalomban van, azzal együtt forog f = 0,4 Hz frekvenciával.
a) Mekkora a test és a korong közt ébredő tapadási erő?
b) Legalább mekkora a korong és a test között a tapadási együttható?
(g = 10 m/s2 )
2024.10.1.
Egy L = 2,4 m hosszú, M = 10 kg tömegű, homogén tömegeloszlású gerendát egy ládára helyezünk, szélére pedig egy kicsiny méretű, m = 5 kg tömegű súlyt teszünk, amint az ábra mutatja.
Legfeljebb mekkora lehet a gerenda x túlnyúlása a láda szélénél, hogy a gerenda ne billenjen le? (Vagy éppen lebillen.)
Legfeljebb mekkora lehet a gerenda x túlnyúlása a láda szélénél, hogy a gerenda ne billenjen le? (Vagy éppen lebillen.)
2016.10.1.
Egy L = 1,5 méter hosszú, M = 2 kg tömegű rudat két harmadoló pontjában támasztunk alá az ábrán látható módon.
Legfeljebb mekkora m tömegű, pontszerű testet tehetünk a rúd szélére, hogy az még ne billenjen le?
Mekkora erő hat az alátámasztási pontokra ekkor?
g = 9,8 m/s2
Mekkora erő hat az alátámasztási pontokra ekkor?
g = 9,8 m/s2
Munka, energia, teljesítmény, hatásfok
2011.05.2.
Egy szivattyú egy perc alatt 200 liter vizet emel ki 3 m mélységből.
A szivattyúzás hatásfoka 40%.
a) Mekkora teljesítményt vesz fel a szivattyú az elektromos hálózatból?
b) Mennyi vizet emel ki ugyanezen szivattyú 5 m mélységből egy óra alatt, ha feltesszük, hogy a szivattyúzás hatásfoka változatlan?
(g = 10 m/s2)
A szivattyúzás hatásfoka 40%.
a) Mekkora teljesítményt vesz fel a szivattyú az elektromos hálózatból?
b) Mennyi vizet emel ki ugyanezen szivattyú 5 m mélységből egy óra alatt, ha feltesszük, hogy a szivattyúzás hatásfoka változatlan?
(g = 10 m/s2)
2012.05.1.
Egy autós egy 16 km-es útszakaszon a megengedett 90 km/h helyett végig 110 km/h sebességgel vezetett.
a) Mennyivel lett rövidebb a menetideje?
b) A közegellenállási erő 110 km/h esetén másfélszerese a 90 km/h mellettinek. 110 km/h esetén a 90 km/h melletti értéknek hányszorosára kell növelni az autó teljesítményét ahhoz, hogy leküzdjük a közegellenállást?
(Ilyen nagy sebesség esetén az egyéb fékező hatások a közegellenálláshoz képest elhanyagolhatóak.)
a) Mennyivel lett rövidebb a menetideje?
b) A közegellenállási erő 110 km/h esetén másfélszerese a 90 km/h mellettinek. 110 km/h esetén a 90 km/h melletti értéknek hányszorosára kell növelni az autó teljesítményét ahhoz, hogy leküzdjük a közegellenállást?
(Ilyen nagy sebesség esetén az egyéb fékező hatások a közegellenálláshoz képest elhanyagolhatóak.)
2017.06.2.
Olvassa el figyelmesen az alábbi szöveget, és a benne található információk segítségével válaszoljon az alábbi kérdésekre!
Gravitációból fényt
A világon körülbelül másfél milliárd család él elektromos áram nélkül. Számukra új, olcsó megoldást talált az esti világításra egy angol mérnök, aki a gravitációt állította a világítás szolgálatába. A lámpa energiaforrása egy láncon függő, 10 kg tömegű, kövekkel vagy homokkal töltött zsák, amelyet 1,8 méter magasba kell felhúzni. Ahogy a zsák lassan leereszkedik egy nagy fogaskereket forgatva, trükkös áttétrendszer segítségével meghajt egy kis egyenáramú generátort, amely percenként több ezres fordulatszámmal forog. A generátor egy szabályozható fényerejű LED-et hoz működésbe. A leadott fényteljesítmény 0,1 W, 0,075 W, vagy 0,05 W.
A középső fokozatban a lámpa 30 percig világít. Ez idő alatt a zsák egyenletesen mozogva a földre ereszkedik, a lámpa ,,lejár”, de a szerkezetet újra működésbe lehet hozni, ha a zsákot ismét felemeljük.
a) Jellemezze energetikailag a lámpa működését! Milyen hasznos energiaátalakulások zajlanak le a lámpa működése közben?
b) A középső fokozatra vonatkozó adatokat felhasználva állapítsa meg, hogy mekkora a lámpa hatásfoka! c) Ha feltételezzük, hogy a lámpa hatásfoka a különböző fényerősségek esetén azonos, milyen hosszú a működési idő az egyes fokozatokban?
(g = 9,81 m/s2)
Gravitációból fényt
A világon körülbelül másfél milliárd család él elektromos áram nélkül. Számukra új, olcsó megoldást talált az esti világításra egy angol mérnök, aki a gravitációt állította a világítás szolgálatába. A lámpa energiaforrása egy láncon függő, 10 kg tömegű, kövekkel vagy homokkal töltött zsák, amelyet 1,8 méter magasba kell felhúzni. Ahogy a zsák lassan leereszkedik egy nagy fogaskereket forgatva, trükkös áttétrendszer segítségével meghajt egy kis egyenáramú generátort, amely percenként több ezres fordulatszámmal forog. A generátor egy szabályozható fényerejű LED-et hoz működésbe. A leadott fényteljesítmény 0,1 W, 0,075 W, vagy 0,05 W.
A középső fokozatban a lámpa 30 percig világít. Ez idő alatt a zsák egyenletesen mozogva a földre ereszkedik, a lámpa ,,lejár”, de a szerkezetet újra működésbe lehet hozni, ha a zsákot ismét felemeljük.
a) Jellemezze energetikailag a lámpa működését! Milyen hasznos energiaátalakulások zajlanak le a lámpa működése közben?
b) A középső fokozatra vonatkozó adatokat felhasználva állapítsa meg, hogy mekkora a lámpa hatásfoka! c) Ha feltételezzük, hogy a lámpa hatásfoka a különböző fényerősségek esetén azonos, milyen hosszú a működési idő az egyes fokozatokban?
(g = 9,81 m/s2)
Folyadékok és gázok
2017.10.2.
Olvassa el figyelmesen az alábbi szöveget, és a benne található információk segítségével
válaszoljon az alábbi kérdésekre!
A batiszkáf
A batiszkáf egy szabadon merülő, meghajtással rendelkező mélytengeri tengeralattjáró, ami egy úszótestből és egy ráfüggesztett legénységi kamrából áll. A rugalmas falú úszótestet benzinnel töltik fel, így annak térfogata gyakorlatilag nem változik, és az úszótest falának nem kell nagy nyomáskülönbséget elviselnie.
Azonban a gömb alakú legénységi kabinnak a nagy mélységben, az utasok védelmében óriási nyomáskülönbséget kell elviselnie, ezért rendkívül masszív felépítésű.
A lemerüléshez a batiszkáf az úszótesthez kapcsolt, levegőt tartalmazó kamrákat áraszt el vízzel, akárcsak a tengeralattjáró. Mivel a nagy mélységben nem képes a vizet ezekből a kamrákból kiszivattyúzni, úgy tud a felszínre emelkedni a jármű, hogy elengedi a ráakasztott vasgolyókból álló úgynevezett ballasztsúlyát.
(A Wikipédia alapján. A kép forrása: wikipedia.org)
a) Hogyan növeli, illetve csökkenti a batiszkáf az átlagsűrűségét a merüléshez, illetve a felemelkedéshez?
b) Miért nem kell az úszótest falának nagy nyomáskülönbséget kiállnia szemben a legénységi kabin falával?
c) Mekkora erőt fejt ki a batiszkáf 50 m3 benzinnel feltöltött úszóteste a legénységi kabinra, ha a batiszkáf a víz alatt egyensúlyban van? (Az úszótest falának súlya és térfogata elhanyagolható.)
(A benzin sűrűsége ρbenzin = 720 kg/m3, a vízé ρvíz = 1000 kg/m3, g = 9,8 m/s2.)
A batiszkáf
A batiszkáf egy szabadon merülő, meghajtással rendelkező mélytengeri tengeralattjáró, ami egy úszótestből és egy ráfüggesztett legénységi kamrából áll. A rugalmas falú úszótestet benzinnel töltik fel, így annak térfogata gyakorlatilag nem változik, és az úszótest falának nem kell nagy nyomáskülönbséget elviselnie.
Azonban a gömb alakú legénységi kabinnak a nagy mélységben, az utasok védelmében óriási nyomáskülönbséget kell elviselnie, ezért rendkívül masszív felépítésű.
A lemerüléshez a batiszkáf az úszótesthez kapcsolt, levegőt tartalmazó kamrákat áraszt el vízzel, akárcsak a tengeralattjáró. Mivel a nagy mélységben nem képes a vizet ezekből a kamrákból kiszivattyúzni, úgy tud a felszínre emelkedni a jármű, hogy elengedi a ráakasztott vasgolyókból álló úgynevezett ballasztsúlyát.
(A Wikipédia alapján. A kép forrása: wikipedia.org)
a) Hogyan növeli, illetve csökkenti a batiszkáf az átlagsűrűségét a merüléshez, illetve a felemelkedéshez?
b) Miért nem kell az úszótest falának nagy nyomáskülönbséget kiállnia szemben a legénységi kabin falával?
c) Mekkora erőt fejt ki a batiszkáf 50 m3 benzinnel feltöltött úszóteste a legénységi kabinra, ha a batiszkáf a víz alatt egyensúlyban van? (Az úszótest falának súlya és térfogata elhanyagolható.)
(A benzin sűrűsége ρbenzin = 720 kg/m3, a vízé ρvíz = 1000 kg/m3, g = 9,8 m/s2.)
2024.10.2.
Hieron király egy 1,93 kg tömegű aranytömböt adott az
aranyművesnek, hogy készítsen belőle koronát.
A korona elkészült, de a király attól tartott, hogy az aranyműves meglopta őt, s az arany egy részét kicserélte ezüstre. Az elkészült korona tömege természetesen pontosan megegyezett a király által adott aranydarab tömegével. A király felkérte Arkhimédészt, hogy döntse el a kérdést, vajon tartalmaz-e ezüstöt is a korona.
Arkhimédész fürdés közben rájött arra, hogy a korona térfogatát pontosan meg tudja mérni annak vízkiszorítása által, ha egy vízzel teli edénybe meríti a koronát. A korona térfogatát összehasonlítva a koronával megegyező tömegű aranydarab térfogatával, az arany és ezüst sűrűségének ismeretében nemcsak a hamisítás tényét, hanem annak mértékét is meg tudta határozni.
a) Írja le részletesen, hogyan lehet egy szabálytalan test térfogatát megmérni vízkiszorítással!
b) Miért tér el az ezüsttel ötvözött korona térfogata a vele megegyező tömegű aranydarab térfogatától?
c) Kimutatható-e a csalás akkor is, ha víz helyett olajat használ a kísérlethez?
d) Az arany sűrűsége 19,3 g/cm3 , az ezüst sűrűsége 10,5 g/cm3 . Hány cm3 a térfogata a király által adott aranydarabnak, és mennyi lenne 1,93 kg ezüst térfogata?
A korona elkészült, de a király attól tartott, hogy az aranyműves meglopta őt, s az arany egy részét kicserélte ezüstre. Az elkészült korona tömege természetesen pontosan megegyezett a király által adott aranydarab tömegével. A király felkérte Arkhimédészt, hogy döntse el a kérdést, vajon tartalmaz-e ezüstöt is a korona.
Arkhimédész fürdés közben rájött arra, hogy a korona térfogatát pontosan meg tudja mérni annak vízkiszorítása által, ha egy vízzel teli edénybe meríti a koronát. A korona térfogatát összehasonlítva a koronával megegyező tömegű aranydarab térfogatával, az arany és ezüst sűrűségének ismeretében nemcsak a hamisítás tényét, hanem annak mértékét is meg tudta határozni.
a) Írja le részletesen, hogyan lehet egy szabálytalan test térfogatát megmérni vízkiszorítással!
b) Miért tér el az ezüsttel ötvözött korona térfogata a vele megegyező tömegű aranydarab térfogatától?
c) Kimutatható-e a csalás akkor is, ha víz helyett olajat használ a kísérlethez?
d) Az arany sűrűsége 19,3 g/cm3 , az ezüst sűrűsége 10,5 g/cm3 . Hány cm3 a térfogata a király által adott aranydarabnak, és mennyi lenne 1,93 kg ezüst térfogata?
2023. 05.A.2.
Infúzió
Nagy felfedezése volt az orvostudománynak, hogy intravénás infúzióval rögtön a beteg vérkeringésébe juttathatnak nagyobb mennyiségű hatóanyagokat. Ahhoz, hogy a gyógyszert tartalmazó folyadék az erekbe juthasson, legalább akkora nyomással kell a folyadékot adagolni, mint amekkora nyomás az erekben uralkodik. Különböző megfontolásokból az infúzió szervezetbe juttatására az artériáknál alacsonyabb nyomású vénás ereket választják. A kar vénáiban a külső légnyomáshoz képest csak mintegy 2400 Pa többletnyomással kell számolni. Vannak olyan berendezések, amelyek elektronikus pumpával adagolják a folyadékot, de a legtöbbször a túlnyomást úgy oldják meg, hogy a gyógyszeres palackot a beteg testénél magasabbra függesztik föl (H magasságban), így a kialakuló hidrosztatikai nyomás biztosítja a szükséges túlnyomást. A gyógyszeres palack alatt egy állítható szűkülettel lehet szabályozni a folyadék áramlási sebességét, amit többnyire nagyon lassúra állítanak, a folyadék csak csepeg. Ha a gyógyszeres palack merev falú, szükség van egy kis szelepre, ami biztosítja, hogy a folyadék helyére levegő áramolhasson, így mindig a külső légnyomás uralkodik a folyadék felett.
a) Hogyan viszonyul egymáshoz a nyomás a vénákban és az artériákban?
b) Ha nem emelik elég magasra az infúziós palackot, a folyadék vérbe jutása helyett a vér fog az infúziós csőben megjelenni. Miért?
c) Mi történne, ha a merev falú, légmentesen zárt palackon nem lenne levegőző szelep? Le tudna-e folyni az infúzió? Válaszát indokolja!
d) Legalább milyen H magasságot kell biztosítani a szöveg szerint, hogy a karban lévő vénába befolyhasson az 1004 kg/m3 sűrűségű infúziós oldat?
(g = 9,8 m/s2 )
Nagy felfedezése volt az orvostudománynak, hogy intravénás infúzióval rögtön a beteg vérkeringésébe juttathatnak nagyobb mennyiségű hatóanyagokat. Ahhoz, hogy a gyógyszert tartalmazó folyadék az erekbe juthasson, legalább akkora nyomással kell a folyadékot adagolni, mint amekkora nyomás az erekben uralkodik. Különböző megfontolásokból az infúzió szervezetbe juttatására az artériáknál alacsonyabb nyomású vénás ereket választják. A kar vénáiban a külső légnyomáshoz képest csak mintegy 2400 Pa többletnyomással kell számolni. Vannak olyan berendezések, amelyek elektronikus pumpával adagolják a folyadékot, de a legtöbbször a túlnyomást úgy oldják meg, hogy a gyógyszeres palackot a beteg testénél magasabbra függesztik föl (H magasságban), így a kialakuló hidrosztatikai nyomás biztosítja a szükséges túlnyomást. A gyógyszeres palack alatt egy állítható szűkülettel lehet szabályozni a folyadék áramlási sebességét, amit többnyire nagyon lassúra állítanak, a folyadék csak csepeg. Ha a gyógyszeres palack merev falú, szükség van egy kis szelepre, ami biztosítja, hogy a folyadék helyére levegő áramolhasson, így mindig a külső légnyomás uralkodik a folyadék felett.
a) Hogyan viszonyul egymáshoz a nyomás a vénákban és az artériákban?
b) Ha nem emelik elég magasra az infúziós palackot, a folyadék vérbe jutása helyett a vér fog az infúziós csőben megjelenni. Miért?
c) Mi történne, ha a merev falú, légmentesen zárt palackon nem lenne levegőző szelep? Le tudna-e folyni az infúzió? Válaszát indokolja!
d) Legalább milyen H magasságot kell biztosítani a szöveg szerint, hogy a karban lévő vénába befolyhasson az 1004 kg/m3 sűrűségű infúziós oldat?
(g = 9,8 m/s2 )
2022.10.A.1.
Egy a = 30 cm élhosszúságú, ρ = 600 kg/m 3 sűrűségű kockát egy mély kádvizébe
helyezünk.
a) Határozza meg, hogy milyen mélyen merül a kocka a vízbe!
b) Mekkora tömegű ólomsúlyt helyezzünk a kockára, hogy a kockát éppen ellepje a víz?
(ρvíz = 1000 kg/m3 , g = 9,81 m/s 2 )
a) Határozza meg, hogy milyen mélyen merül a kocka a vízbe!
b) Mekkora tömegű ólomsúlyt helyezzünk a kockára, hogy a kockát éppen ellepje a víz?
(ρvíz = 1000 kg/m3 , g = 9,81 m/s 2 )
2020.05.1.
Az ősmaradványok tanúsága szerint egy bizonyos fajta dinoszaurusz feje a szívénél
20 méterrel volt magasabban, a szív a talaj felett 8 m magasságban helyezkedett el.
a) Legalább mekkora nyomással kellett a szívének a vért pumpálnia, ha a dinoszaurusz agyának (ami a fejében volt) legalább 11000 Pa vérnyomásra volt szüksége?
b) Mekkora volt ekkor a vérnyomás a dinoszaurusz lábában?
A vér sűrűsége ρ = 1060 kg/m3 , g = 9,8 m/s2
a) Legalább mekkora nyomással kellett a szívének a vért pumpálnia, ha a dinoszaurusz agyának (ami a fejében volt) legalább 11000 Pa vérnyomásra volt szüksége?
b) Mekkora volt ekkor a vérnyomás a dinoszaurusz lábában?
A vér sűrűsége ρ = 1060 kg/m3 , g = 9,8 m/s2
Rezgések és hullámok
2013.06.1.
Egy varrógéptű varrás közben függőleges egyenes mentén harmonikus rezgőmozgást végez.
Mozgása legalsó és legfelső pontja között 4 cm a távolság.
A gép 9 másodperc alatt 24 öltést ejt.
a) Mekkora a tű legnagyobb sebessége és a legnagyobb gyorsulása?
b) Tegyük fel, hogy a cérna egy 1 cm átmérőjű, lassan elforduló cérnaorsóról tekeredik le. Hányat fordul egy perc alatt a cérnaorsó, ha egy öltéshez 4 mm cérnára van szükség?
(A varrógép tűje a rezgés egy teljes periódusa alatt egy öltést készít el.)
Mozgása legalsó és legfelső pontja között 4 cm a távolság.
A gép 9 másodperc alatt 24 öltést ejt.
a) Mekkora a tű legnagyobb sebessége és a legnagyobb gyorsulása?
b) Tegyük fel, hogy a cérna egy 1 cm átmérőjű, lassan elforduló cérnaorsóról tekeredik le. Hányat fordul egy perc alatt a cérnaorsó, ha egy öltéshez 4 mm cérnára van szükség?
(A varrógép tűje a rezgés egy teljes periódusa alatt egy öltést készít el.)
2022.05.C.1.
A szeizmika tudománya mesterségesen keltett rengéshullámokkal tanulmányozza
a Föld belső szerkezetét.
Egy felszín alatti, de a felszínnel párhuzamos kőzetréteg mélységét szeretnénk meghatározni a kőzethatárról visszaverődő hullámok segítségével.
Az elrendezésünk az egyszerűség kedvéért egy robbantási pontból (R) és ettől a ponttól d1 = 50 m és d1 = 100 m távolságban elhelyezkedő két rezgésérzékelő geofonból (G 1 és G 2) áll.
A robbantási pont és a két geofon egy egyenesbe esnek.
Az elrendezést az ábra mutatja. A robbanás során keltett hullám az alsó rétegről visszaverődik, és ezt észlelik a geofonok.
A csatolt táblázat a robbantás és a visszavert hullám beérkezése között eltelt időt mutatja a két geofon esetében.
A másik táblázatban a hullám terjedési sebességét adtuk meg a különböző kőzetekben.
a) Milyen mélységben van az alsó kőzetréteg?
b) Mekkora sebességgel terjed a hullám a felső kőzetrétegben?
Milyen anyag alkotja a felső réteget?
Egy felszín alatti, de a felszínnel párhuzamos kőzetréteg mélységét szeretnénk meghatározni a kőzethatárról visszaverődő hullámok segítségével.
Az elrendezésünk az egyszerűség kedvéért egy robbantási pontból (R) és ettől a ponttól d1 = 50 m és d1 = 100 m távolságban elhelyezkedő két rezgésérzékelő geofonból (G 1 és G 2) áll.
A robbantási pont és a két geofon egy egyenesbe esnek.
Az elrendezést az ábra mutatja. A robbanás során keltett hullám az alsó rétegről visszaverődik, és ezt észlelik a geofonok.
A csatolt táblázat a robbantás és a visszavert hullám beérkezése között eltelt időt mutatja a két geofon esetében.
A másik táblázatban a hullám terjedési sebességét adtuk meg a különböző kőzetekben.
a) Milyen mélységben van az alsó kőzetréteg?
b) Mekkora sebességgel terjed a hullám a felső kőzetrétegben?
Milyen anyag alkotja a felső réteget?
| G1 | G2 | |
| A geofon távolsága az R ponttól (d) | 50 m | 100 m |
| A robbanás és a jel beérkezése között eltelt idő (t) | 0,044 s | 0,066 s |
| Kőzet neve | A hullám jellemző terjedési sebessége a kőzetben (m/s) |
| homokkő | 2000-4500 |
| mészkő | 3400-6000 |
| agyag | 1100-2500 |
| kősó | 4000-5500 |
| gránit | 5000-6200 |
2019.06.2.
Zenehallgatás útközben
Bárki hallhatta már autóval megfelelő sebességgel haladva, hogy a különböző típusú útburkolatokon más-más hangot ad ki az autó. Sima úton halkan fut, szinte siklik. Egyenetlen felületű útra érve az autó érezhetően finoman rezegni kezd a korábbi siklás helyett. Pont ezt a jelenséget használták ki elmés szakemberek, amikor megfelelő távolságokra keresztirányú, párhuzamos bemarásokat vagy kiemelkedő bordákat készítettek az út felületére. Ezek rezgéseket keltenek a rajtuk haladó autóban. A karosszériában keletkező rezgés pedig az utastér levegőjében hangot kelt. A hang magassága a barázdák egymástól való távolságától és az autó sebességétől függ.
A tervek szerint a 67-es főút (mely Balatonszemest Szigetvárral köti össze) egyik szakaszára ilyen zenélő aszfalt kerül, mely a Republic együttes „A 67-es úton” című dalát fogja játszani. A kép egy megvalósult japán zenélő utat ábrázol.
Kép forrása: http://www.gitarpengeto.hu/zenei-utazasi-ajanlat/dalol-az-aszfalt-ut-japanban/ a) Képzeljük el, hogy az ábrán látható úton egy autó halad a hozzánk közelebbi bordákon balról jobbra. (Mind a négy kereke a felénk eső bordákon halad.) Hogyan változik a hang magassága, amikor a sűrűbben bordázott szakaszhoz ér? Válaszát indokolja!
b) Hogyan befolyásolja a hang magasságát a barázdákon futó autó sebessége? Válaszát indokolja!
c) Ha egy autó 90 km/h sebességgel halad, mekkora legyen a barázdák távolsága, hogy 250 Hz-es hangot halljunk?
Bárki hallhatta már autóval megfelelő sebességgel haladva, hogy a különböző típusú útburkolatokon más-más hangot ad ki az autó. Sima úton halkan fut, szinte siklik. Egyenetlen felületű útra érve az autó érezhetően finoman rezegni kezd a korábbi siklás helyett. Pont ezt a jelenséget használták ki elmés szakemberek, amikor megfelelő távolságokra keresztirányú, párhuzamos bemarásokat vagy kiemelkedő bordákat készítettek az út felületére. Ezek rezgéseket keltenek a rajtuk haladó autóban. A karosszériában keletkező rezgés pedig az utastér levegőjében hangot kelt. A hang magassága a barázdák egymástól való távolságától és az autó sebességétől függ.
A tervek szerint a 67-es főút (mely Balatonszemest Szigetvárral köti össze) egyik szakaszára ilyen zenélő aszfalt kerül, mely a Republic együttes „A 67-es úton” című dalát fogja játszani. A kép egy megvalósult japán zenélő utat ábrázol.
Kép forrása: http://www.gitarpengeto.hu/zenei-utazasi-ajanlat/dalol-az-aszfalt-ut-japanban/ a) Képzeljük el, hogy az ábrán látható úton egy autó halad a hozzánk közelebbi bordákon balról jobbra. (Mind a négy kereke a felénk eső bordákon halad.) Hogyan változik a hang magassága, amikor a sűrűbben bordázott szakaszhoz ér? Válaszát indokolja!
b) Hogyan befolyásolja a hang magasságát a barázdákon futó autó sebessége? Válaszát indokolja!
c) Ha egy autó 90 km/h sebességgel halad, mekkora legyen a barázdák távolsága, hogy 250 Hz-es hangot halljunk?